How Big is a Proton? Barns, femtobarns, and the LHC.
/If you try to follow the conversation physicists have about physics at a particle collider like the Large Hadron Collider (LHC), you'll see people talking about things call picobarns, femtobarns, and inverse femtobarns. What are they talking about?
A "barn" is just a unit of area, like a square foot, a square meter, or an acre. It's just a very small unit of area. One barn is 10-28 square meters, or 1.07x10-27 square feet. And let's be honest, that probably isn't a useful quantity for you. Honestly, though I have an idea of a barn as a relative unit size, that's only because I spend a lot of time thinking about the quantum world. The jump from things measured in barns to things measured in more quotidian units is difficult.
Let me put it this way. A human hair is about 20 micrometers in diameter. Which means if you slice it in half, each strand has a surface area of 3x10-10 m2. Or 3x1018 (3 million trillion) barns.
So what possible use is a barn? And why on Earth is it called a barn?
Barns are used as cross sections. A cross sectional area is just the surface area that an object presents when you look at it from a certain angle. You can think of it as "the area through which you'd have to throw something in order to hit the object."
SKetch of the cross sectional area of a sphere of radius r. Red and Blue shaded regions are the cross section looking from the side and top, respectively.
So a sphere of radius r presents the same cross section no matter how you look at it: it is always π r 2 . Now, if you take something that isn't perfectly symmetrical, then the cross section depends on how you look at it. A person, for example, has a relatively small cross section if you were looking down at their head (basically, just the area projected by their head and shoulders), but a larger cross section if you are looking at them face-on (then the cross section is the area projected over their whole body). Since the cross section is an area, we measure it in square meters, assuming we're used to SI units.
So, why is cross section a useful concept to think about?
Imagine you had a box that you couldn't look into, but you knew there was some mystery object inside of. Imagine further you could throw little balls into the box from any angle, and measure whether they came back out, and if so, in which direction.
Then, if you were patient and had enough ammo, you could figure out a lot about the mystery object. If you threw balls in, and they came out of the box directly opposite of where you threw them in, you can guess that you missed the object entirely. Eventually, you'll start having ammunition thrown in that comes out at odd angles, after ricochetting off of the target. Not only could you map out the total cross section of the object from every angle, you could map out the differential cross section : how often you throw a ball in and have it come out heading in exactly this direction instead of that direction.
Sketch of technique to map out cross section of an unknown object using test ammunition.
OK, that sounds clever perhaps, but pretty useless on a day to day basis. I mean, how often do you have a box you can't look inside but can throw things into from any direction?
Well, in case you haven't figured it out from the fact you're on a website written by a guy who calls himself physicsmatt, this is how we figure out the "shape" of atomic and subatomic particles. We can't see such small objects like a proton, but we can throw things at them (photons, electrons, other protons) and measure the deflection of those objects, and use that to determine the properties of those particles. One oddity of subatomic particles is that their size is different depending on what ammunition you use; this is because different particles feel different forces, so an electron scattering off a proton, say, has to "hit" a smaller area than a proton hitting another proton.
This is actually how the name "barn" came about. A barn is approximately the cross sectional size of a large atom (specifically a uranium nucleus) as seen by protons and neutrons. During the early days of the atomic program, American physicists discovered that the uranium atom was really large; at least as far as incredibly microscopic objects go. Everything they threw at it seemed to "hit," so the nucleus was "as big as a barn." Plotted in SI units, this barn-sized object was about 10-28 m2, so the physicists decided, hey, let's call that a barn, and not have to write an exponent every time. Convenient. And is what passes for humor amongst physicists.
At the LHC, most of the year, protons are collided against other protons. As you throw protons together at different energies, their effective "size" changes, but at LHC energies, a proton is about a tenth of a barn in cross section. This is a pretty big size, due to the fact that the protons interact via the strong nuclear force. This strong force is, you guessed it, strong. This means that it presents a "big" target, when compared to interactions that are "weaker," like the weak nuclear force or the electromagnetic force.
Indeed, the "size" of a proton at the LHC to interact via the weak nuclear force with another proton is about 1 million times smaller, something like 100 nanobarns (100 nb). That means that you have to "hit" something a million times smaller to have the interaction go through the weak nuclear force rather than the strong nuclear force.
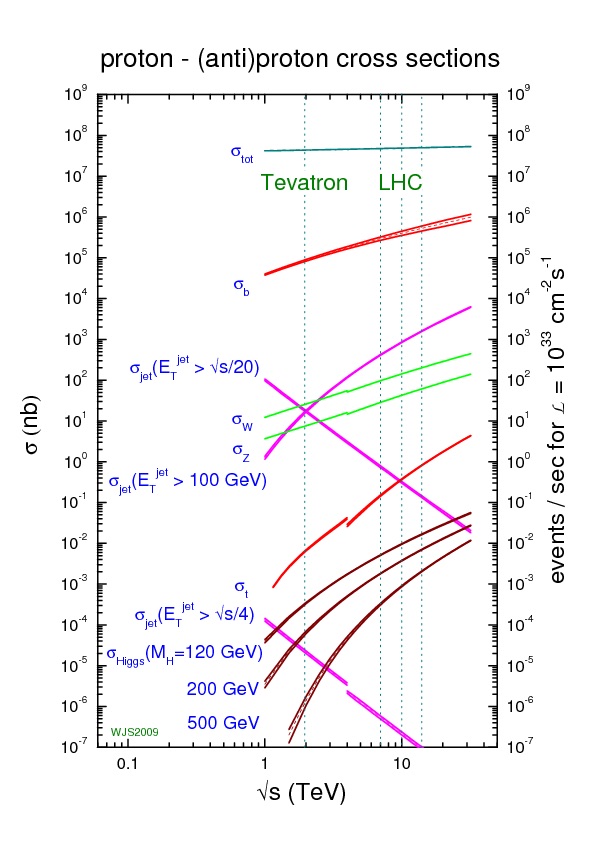
Cross Sections of representative processes at the LHC. From Plehn 0910.4182
And this is the real utility of cross sections. Quantum mechanics means that there is no way for us to know ahead of time exactly what will happen when you throw two protons together. Maybe they will interact via the strong force, maybe the weak force. There's no deterministic way to know what will happen. But on average, if you want to know how often each type of process will occur, you just divide by the relative cross sections.
Indeed, you can even ask "how big of an area do you have to hit in order to create a particular new particle?" Again, there's no Magic Zone on a proton that if you physically hit it with another proton, you'll get something new every time; at quantum scales, protons don't even really exist at a particular point like we're used to thinking about particles. However, the metaphor is very useful.
I'm showing here a plot of cross sections (in nb) for various processes at proton-proton colliders for different collision energies (the LHC started at 7 TeV, then went to 8, and is moving to 13 TeV on the x-axis). The total interaction cross section is about 108 nb. The cross section to cause a jet of strongly interacting particle to go shooting off with 100 GeV of "sideways" momentum is about 103 nb, meaning that one out 10,000 events will have such a jet of energy. The cross section to produce a Higgs with a mass of 120 GeV (close to the true value of 125 GeV, this plot was made at least 3 years before we know the mass of the Higgs) is about 10-2nb, or 10 pb. So only one out of ten billion events or so will produce a Higgs. Again, we can think of this as two protons hitting each other in some tiny little area, as long as we don't take that metaphor too seriously.
So that's cross sections. It's a very useful way of thinking about really unusual objects: subatomic particles. The other thing you'll see in LHC physics is something with inverse cross sections as a unit. Something like an inverse picobarn, or an inverse femtobarn. What do we mean by that?
Well, we throw a lot of protons together. We can talk about the luminosity of the beam, the number of protons delivered to the collision zone per second, or the total number of protons that have passed through and had data taken about any collisions that happened. How best to represent that number of protons? I could tell you how many protons, but that's not that useful, since if the protons are far apart from each other, then the probability of collision is low. Really I want the number of protons per some area per second. Huh, that's a unit of inverse area (a barn) per time.
What we really want to know is just how many interesting things happened. We can characterize interesting by the cross section of that interesting event. A Higgs production event is interesting, for example, so we want to know how many things with a cross section of 10 pb happened at the LHC.
If I tell you the luminosity as "inverse pb per second" or "inverse pb for the whole run of the LHC," then the number of events of a particular type that happened (on average) is just cross section times luminosity in those units. The LHC delivered 20 fb-1 over the first data-collection run. That is, 20,000 pb-1. Given a Higgs production cross section of 10 pb, that means we expect to have produced 10x20,000 = 200,000 Higgs events. Easy to figure out, once you see why we use these units.
Of course, not all of those Higgses will be "useful." Some might not have enough sideways push to make a big enough splash in the detector, or decayed into things we have difficulty seeing. Figuring out how many useful events you get depends on the differential cross sections; how big of an area you have to hit to kick out a Higgs that has the right properties to be seen. The full answer is a complicated problem, required knowledge of what is possible to see at a detector at the LHC, and usually is solved by using simulation tools. That sort of thing is the job of experimentalists, and also the sort of thing phenomenologists, or theoretical physicists who spend a lot of time thinking about what will be found at a collider and how to find it, concern themselves with. In addition to astrophysics, phenomenology is one of the theoretical physics hats I wear, on occasion.